Multiplier des nombres en écriture égyptienne
Multiplication par 10 : il suffit de remplacer chaque symbole par celui qui lui est supérieur.
 |
devient |
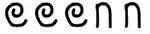 |
Multiplication par un nombre quelconque : les égyptiens n’utilisaient que la multiplication par 2 et se servaient de la distributivité par rapport à l’addition. Il s’agissait de décomposer le plus petit facteur en la somme de puissances de 2 (1, 2, 4, 8, 16, 32, 64 …). Pour éviter de faire chaque fois de nombreux calculs, ils créaient des tables contenant un grand nombre de puissances de 2 dont ils se servaient à chaque calcul.
Pour décomposer un nombre en une somme de puissances de 2, ils trouvaient d’abord la plus grande puissance de 2 inférieure ou égale au nombre, la soustrayaient, et recommençaient jusqu’à ce qu’il reste "rien" (les égyptiens n’utilisaient pas le zéro !).
Exemple avec nos chiffres actuels : 238 × 13
-
La plus grande puissance de 2 inférieure ou égale à 13 est 8,
-
13 – 8 = 5
-
La plus grande puissance de 2 inférieure à 5 est 4,
-
5 – 4 = 1
-
La plus grande puissance de 2 inférieure à 4 est 1 ,
-
1 – 1 = rien.
13 est donc la somme de 8, 4 et 1 : 13 = 8 + 4 + 1
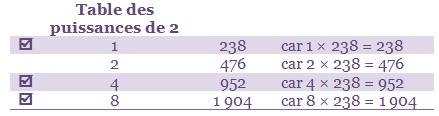
Ensuite ils construisaient la table des puissances de 2 du deuxième facteur, en passant d’une ligne à l’autre en la multipliant par 2:
Puis ils additionnaient tous les nombres de la deuxième colonne dont la puissance de 2 correspondante fait partie de la décomposition du premier facteur :
13 = 8 + 4 + 1 donc 13 × 238 = (8 + 4 + 1) × 238 = 8 × 238 + 4 × 238 + 1 × 238 = 1 904 + 952 + 238
Donc : 13 × 238 = 3 094
Deuxième exemple : 327 × 145
145 – 128 = 17
17 – 16 = 1
1 – 1 = rien.
145 = 128 + 16 + 1. |
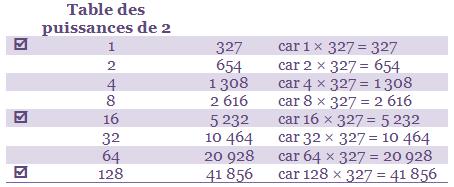 |
Donc : 327 × 145 = 41 856 + 5 232 + 327 = 47 415
retour à la page d'accueil de la numération égyptienne