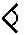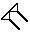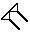Les numérations babyloniennes
La civilisation babylonienne est l’une des plus anciennes civilisations connue à ce jour. Elle a débuté vers 5 000 ans avant Jésus-Christ, jusqu’au début de notre ère, connaissant son apogée entre 1792 et 1750 avant Jésus-Christ.
A l’origine, deux peuples ethniques, les Akkadiens et les Sumériens (ce sont les premiers à avoir utilisé l’arithmétique), vont donner naissance aux civilisations antiques d’Akkad et d’Assyro-Babylonie, puis au Grand Empire de Babylone, qui dominera pendant longtemps la région avant les conquêtes Perse et Macédonienne.
Babylone était située dans l’ancienne Mésopotamie (actuel Irak), bâtie il y a 2 500 ans à 100 km de Bagdad. La Mésopotamie (du grec Mesos – qui signifie milieu – et Potamos – qui signifie fleuve –), était une zone qui s’étendait entre les fleuves du Tigre et de l’Euphrate (le territoire est aujourd’hui partagé entre l’Irak et la Syrie).
Deux systèmes de numération sont à distinguer : la numération assyro-babylonienne et la numération savante babylonienne.
Si ces deux systèmes comportent deux symboles pour les chiffres de base, seule la numération assyro-babylonienne comporte des symboles spécifiques pour les nombres 100 et 1 000.
Les deux symboles communs sont le clou :  et le chevron :
et le chevron : 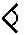 .
.
Pour 100 dans la numération assyro-babylonienne, ils accolaient un clou vertical et un clou horizontal, pour 1 000, ils juxtaposaient un chevron, un clou vertical et un clou horizontal.
Numération assyro-babylonienne
Ce système repose sur une décomposition du nombre selon ses puissances de 10, c’est donc une numération décimale. On marque un espace entre chaque ordre.
Exemple : 3 422 = (1 + 1 +1) × 1 000 + (1 + 1 + 1 + 1) × 100 + (1 + 1) × 10 + (1 + 1)
Ce qui donnait :

Cette numération s’est progressivement enrichie avec la notation des milliers (le millier est alors considéré comme une unité de compte) grâce au principe multiplicatif.
Exemple : 304 212 = (1 + 1 +1) × 100 × 1 000 + (1 + 1 + 1 + 1) × 1 000 + (1 + 1) × 100 + 1 × 10 + (1 + 1)
Ce qui donnait :
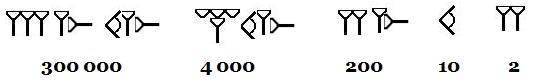
Numération savante babylonienne
C’est la première apparition d’un système de position (comme notre système actuel), inventé par les savants babyloniens à partir de l’an 2 000 avant Jésus-Christ.
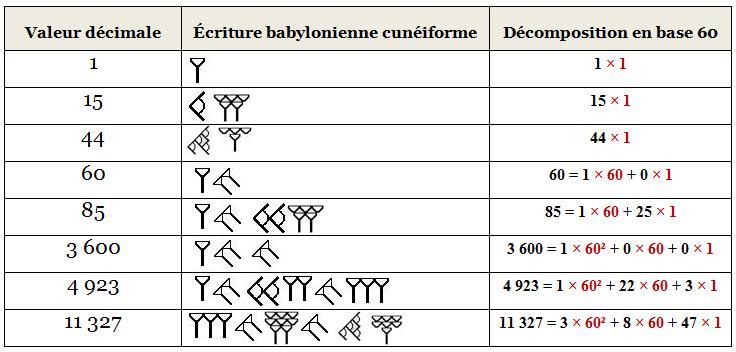
Il s’agit d’un système sexagésimal (en base 60 – notre système est en base 10), c'est-à-dire que chaque nombre est décomposé selon un principe additif de puissances de 60 (1 ; 60 ; 60² = 60 × 60 = 3600 ; 603…) . A ce titre, il est intéressant de noter que c’est des Babyloniens que nous avons hérité l’usage de diviser les heures en 60 minutes, les minutes en 60 secondes, et la circonférence d’un cercle en 360°.
Pourquoi ont-ils choisi d’utiliser la base 60 me demanderez-vous? Tout simplement pour faciliter les calculs avec les fractions, car 60 possède un très grand nombre de diviseurs.
En résumé, pour écrire en numération savante babylonienne :
-
de 1 à 9, les chiffres sont obtenus par itération du symbole
|
 . . |
On remarquera que les Babyloniens n’écrivaient pas plus de 3 clous consécutifs, mais les superposaient, par gain de place.
-
de 10 à 59, on répète autant de fois que nécessaire les symboles
|
 |
et |
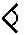 |
, par addition. |
-
60 s’écrit aussi avec le symbole
|
 |
(d’où des confusions de lecture évidentes). |
-
A partir de 61, c’est le système de numération de position qui est appliqué, comme pour notre propre système de numération : la première colonne à droite correspond aux unités, la deuxième aux soixantaines, la troisième au rang des 60 × 60, la quatrième au rang des 60×60×60 etc …
-
Et pour éviter des confusions entre les nombres des colonnes, les savants Babyloniens ont eu l’idée (bien tardive !) de
-
|
créer un symbole pour représenter le rien (à la place de l’espace vide qu’ils laissaient auparavant) : |
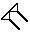 |
. Néanmoins, ce |
symbole ne fut pas considéré comme un « zéro » mais bien comme un symbole pour marquer un espace vide.
Exemples de nombres écrits en numération babylonienne : attention, dans mes écritures babyloniennes, j’ai volontairement utilisé le symbole du « rien » (pourtant arrivé bien plus tardivement) afin d’éviter toute confusion de lecture.
|
Imaginez maintenant que je n’aie pas mis le symbole du vide : |
 |
, les nombres 1 ; 60 ; et 3 600 par exemple, auraient la |
|
même écriture: |
 |
, et il vous serait difficile de pouvoir dire le nombre que j’ai choisi au départ. Mais alors comment |
faisaient-ils avant l’invention de ce symbole ? Et bien tout dépendait du contexte dans lequel apparaissaient les nombres !

Tablette d’argile datant de l’an 2350 av. J.-C.
Comptes de chèvres et de moutons |
 et le chevron :
et le chevron : 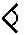 .
.
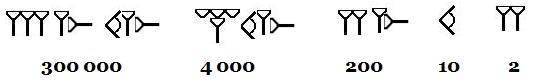
 .
.