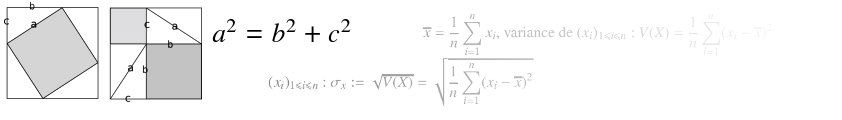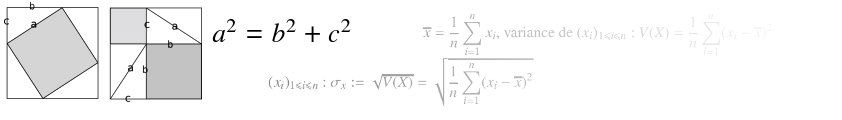Opérations chez les savants babyloniens
L’addition et la soustraction ne posaient pas de problème. L’utilisation d’une numération de position (où chaque nombre a un ordre propre) permettait en effet de calculer très rapidement, notamment avec des petits nombres nécessaires pour commercer par exemple.
Pour les multiplications avec les nombres entiers, les Babyloniens se servaient de tablettes d’argile sur lesquelles figuraient les tables des premiers carrés d’entiers, (comme l’attestent deux tablettes trouvées à Senkerah sur l’Euphrate en 1854, datées de 2000 av. J.-C., qui représentent des listes de carrés d’entiers jusqu'à 59 et de cubes jusqu’à 32) puis utilisaient des considérations géométriques (calculs d’aire de rectangle et de carrés) afin d’effectuer leurs opérations. Cette méthode nécessite uniquement de savoir faire des additions, des soustractions et une table des carrés. |

Tablette d'argile représentant des multiplications |
Exemple de multiplication d’entiers : calcul de 22 × 14
Donc, 22 × 14 = 14 × 14 + 8 × 8 + 6 × 6 + 2 × 2 + 2 × 2 + 2 × 2.
Finalement, 22 × 14 = 196 + 64 + 36 + 4 + 4 + 4 = 308
Dans les cas où ils ne pouvaient pas décomposer le produit en une somme de carrés, les Babyloniens utilisaient alors ce que l’on appelle aujourd’hui les identités remarquables :
Exemple de multiplication d’entiers : calcul de 9 × 15
9 × 15 = [(9 + 15)² – 9² – 15²] : 2 = (24² – 9² – 15²) : 2 = (576 – 81 – 225) : 2 = 270 : 2 = 135
Preuve géométrique telle que l’utilisaient les Babyloniens :
On peut aussi imaginer que les savants Babyloniens connaissaient et utilisaient cette égalité, qui se démontre facilement de nos jours avec les identités remarquables :
9 × 15 = [(15 + 9)² – (15 – 9)²] : 4 = (24² – 6²) : 4 = (576 – 36) : 4 = 540 : 4 = 135
Enfin, les Babyloniens ne posaient pas les divisions. Ils utilisaient la multiplication par l’inverse (résultat bien connu de nos jours : « diviser par un nombre, c’est multiplier par son inverse »).
Ils avaient pour ce faire créé des tables d’inverses de nombres entiers.
Pour les savants Babyloniens, deux nombres sont inverses l’un de l’autre si leur produit est une puissance de 60. (par
|
exemple, l’inverse de |
 |
(2) est |
 |
(30) car 2 × 30 = 60). |
Sur la table classique d’inverse, on pouvait lire par exemple : 8 7 :30 ce qui signifiait que l’inverse de 8 était 7 : 30 ou
7 × 60 + 30 (en base 60) car 8 × (7 × 60 + 30) = 8 × 450 =3 600 = 60², une puissance de 60.
Exemple de table telle qu’elle devait être écrite puis traduction dans notre numération:
Traduction dans notre numération :
La ligne surlignée indique que l’inverse de 18 (pour les Babyloniens) est le nombre : 3×60+20=1800+20=1820
Vous allez maintenant voir sur un exemple simple (432 :18) à quels calculs complexes cette méthode conduisait :
Autres travaux babyloniens
 |
 |
 |
Tablette Plimpton 322
Université Columbia
tablette d'argile datée d'entre 1822 et 1784 avant J.-C. sur laquelle pourraient être représentés des triplets pythagoriciens, c'est à dire trois nombres a, b et c tels que a²+b²=c² |
Tablette YBC 7289
Université Yale
tablette d'argile datée d'environ 1800 avant J.-C., donnant la racine carrée de 2 avec quatre chiffres sexagésimaux significatifs, soit près de six chiffres décimaux :
1 + 24/60 + 51/602 + 10/603 = 1,41421296 |